After deep-diving into why SAEs succeed at retrieving superposed features, what their limitations are, and closely inspecting the hidden technical implementations of the sae_lens library, I just wanted to write some quick notes of what I think the MLP space looks like, with respect to ‘true’ features.
Anticorrelated (“Mutually Sparse”) Features Prefer to be in the Same Tegum Factor
This hypothesis of mine is essentially motivated by 2 things:
- Anticorrelated features generally do not co-activate. This means that you can train an auto-encoder to encode all of those features in the same low-dimensional latent space and be able to extract them without loss (the really basic Anthropic ReLU Toy Model with one-hot input vectors; since they are one-hot, all the features are mutually sparse).
- Once you start adding in density (feature co-activation), auto-encoders generally start preferring PCA solutions, meaning that they will start to learn principle components (orthogonal features) of the dataset.
Findings that corroborate my hypothesis: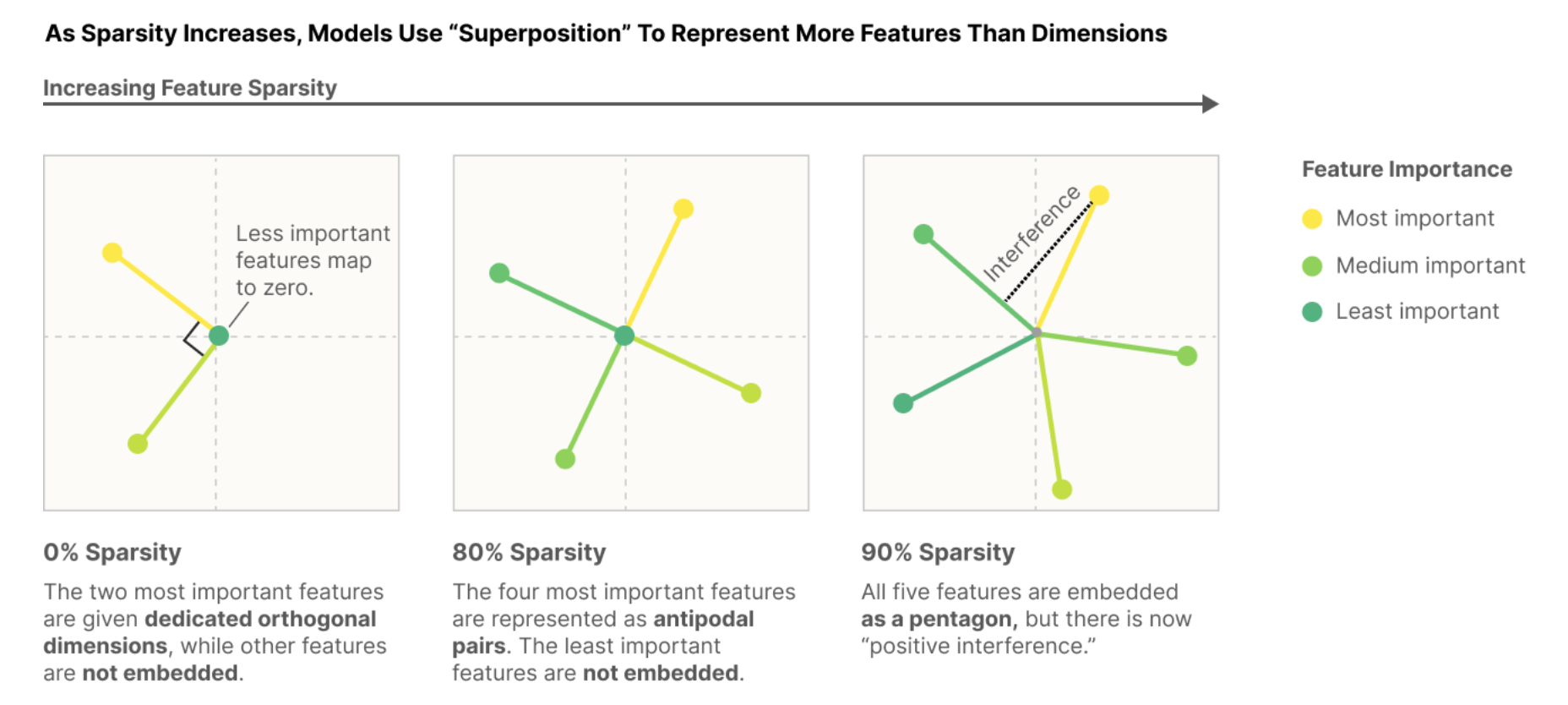 
From Toy Models of Superpositions, Anthropic
And what I’m saying is also a generalized version of what Anthropic is saying in this graphic: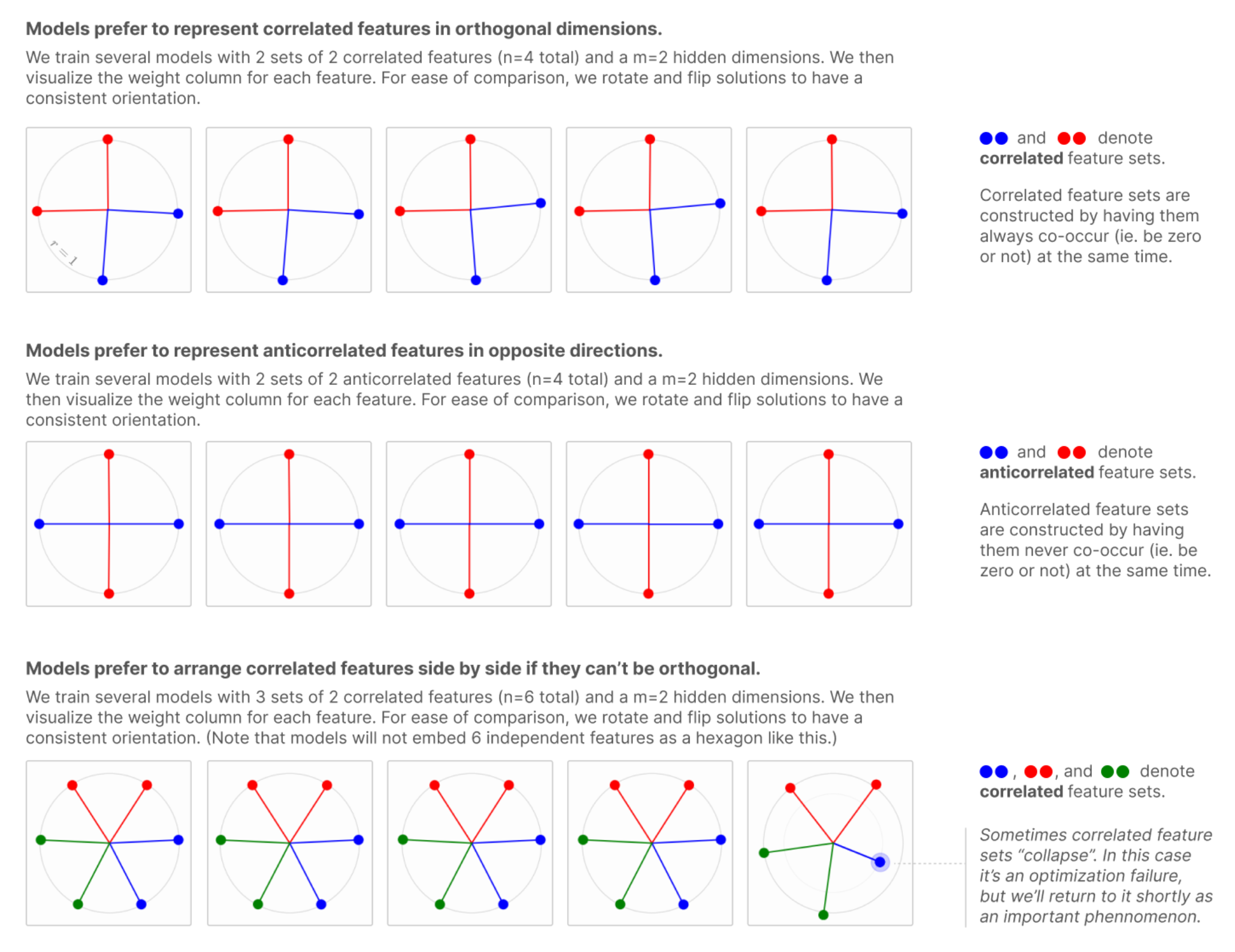 
From - you guessed it - Toy Models of Superpositions, Anthropic
Tegum Factors are generally Not Regular Polytopes
The title of this section. This is because in general, features are not equal; they occur with different frequencies, different pairwise correlations, different magnitude variances, and so on. A tegum factor hence just refers to a polytope that is constrained to some number of dimensions, and I find it useful to talk about tegum products because in a tegum product of tegum factors, the tegum factors do not overlap in dimensions.
The MLP space is Entirely a Tegum Product of Tegum Factors
While in general, the MLP space is never a perfect Tegum Product of Tegum Factors (because deep models are trained via iterative / numerical methods), it is my intuition that this organization of MLP space presents a very strong (possibly the best) local optimum. Again, this is a hypothesis corroborated by some plots that Anthropic made:
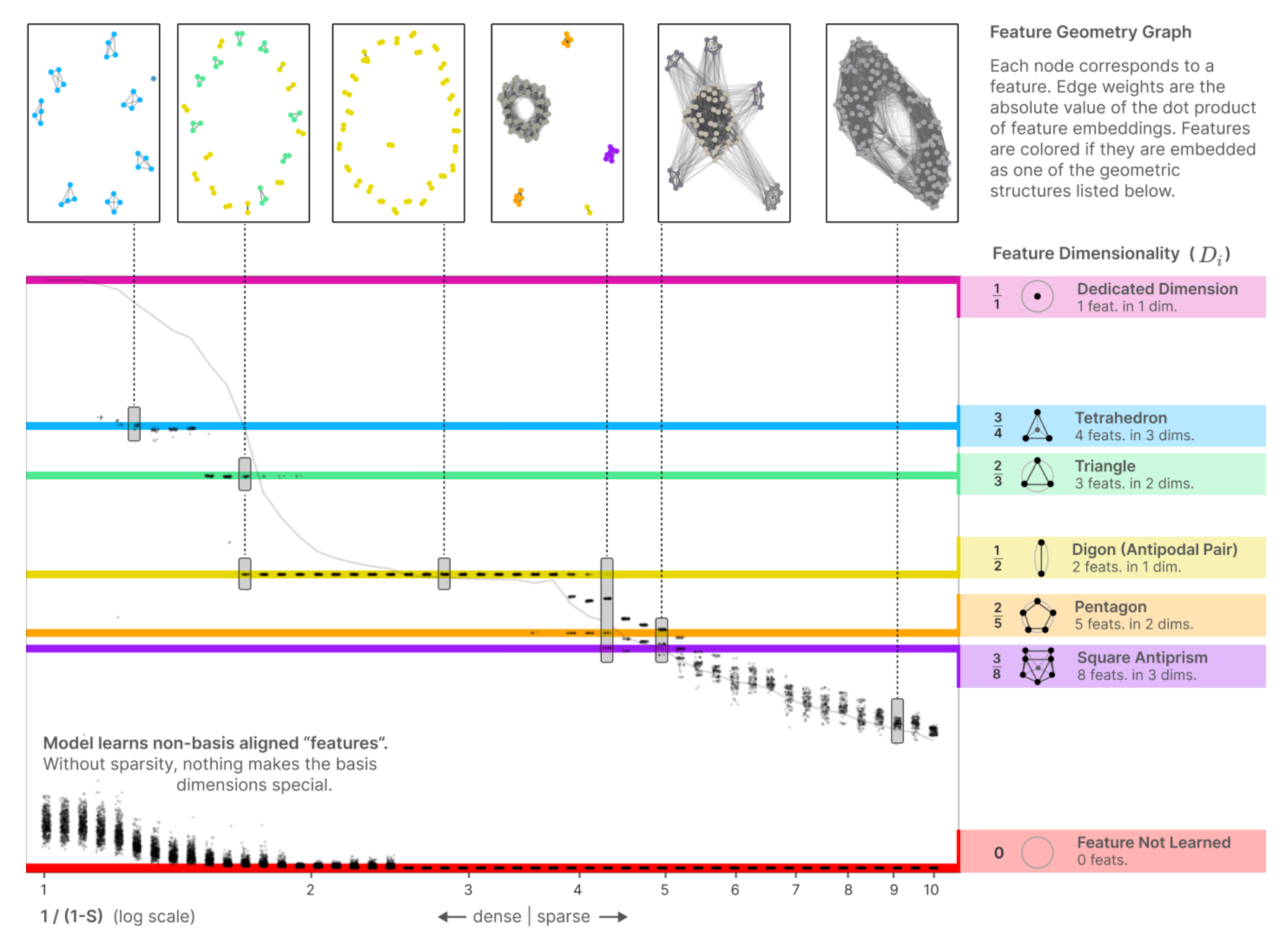From Toy Models of Superpositions, Anthropic again
How does this help with SAE training?
Suppose there is some universe of true features, and the universal feature activation $u$ is defined as follows:
\[u \in \mathbb{R}^{\texttt{d_u}}\]Further suppose that the MLP activations ($x$) you see are some compression of $u$:
\[x = U u, U \in \mathbb{R}^{\texttt{d_mlp} \times \texttt{d_u}}\]Further, without loss of generality, suppose I told you that the first 5 entries of $u$ are compressed into the same tegum factor, and the tegum factor is 3 dimensional. Then, the subspace of this tegum factor is spanned by the first 5 columns of $U$, such that $U_1$ to $U_5$ are the stems of the trigonal bipyramidal polytope (suppose the tegum factor is regular).
I now give you a dataset $X’$ that I tell you is entirely made up of features in this tegum factor. Suppose you follow my intuition of tegum factors having anti-correlated features, and so the dataset $X’$ must be mostly one-hot in the feature basis. Extracting these 5 features is trivial with the L1 loss.